Single-molecule biophysics

Optical trapping (optical tweezers) is an interesting and rather novel technique (first demonstrated by Ashkin in 1970) where the light pressure created by a laser is used to hold and manipulate various microobjects under a microscope. The principle is rather simple. When focusing intense light through a microscope objective, the rays above and below the focal point form a shape that, in an ideal approximation (in case of an infinitely small focal point), form something like a (double) cone. Now consider an object, e.g. a sphere, having a refractive index different from the overall environment, that is put inside this light cone. Rays passing through the object have to refract twice -into and out of the object, which generally involves a change of the rays’ direction. But we must keep in mind that a ray of light may also be regarded as a flux of light particles-photons, and that photons also carry a momentum. Now if the direction of motion (and hence the momentum) of the photons is changed while passing through the spherical object, the law of conservation of momentum states that some momentum must be given to the particle, too. It turns out that if the refractive index of the sphere is greater than that of the surrounding environment then the arising net momentum always pushes the sphere towards the focal point (see the figure below) and fixes it there (in fact, the equilibrium position is slightly further from the focal point because of the photons that reflect back from the front surface of the sphere).

It is clear that the momentum of a photon is very small in the scale of moving macroscopic objects, even if those measure in microns. Therefore, for such a scheme to work, the light intensity has to be rather high. Also, an objective with a high numerical aperture value has to be used so the angle spanned by the cone is greater and the photons travelling along its outer surface undergo a larger vectorial momentum change when passing through the object. The trapped particle must be neither too big (causing its mass and viscous drag from the surroundings be too large) nor too small (insufficient momentum change).

Our setup-currently still very much under development-uses a 1064 nm, 1W output Nd:YAG laser, giving a power of about 200 mW out of the objective. We use an Olympus IX-71 microscope with a 100x oil immersion objective having a numerical aperture of 1.3 (the corresponding cone angle is 118°). As test objects, we have used e.g. baking yeast cells, having a diameter of 5-6 µm. In this case it is hard to estimate the difference of its refractive index from that of the surrounding medium (water), but it’s probably not too large, as the cell’s refraction is mostly dominated by water, too. Nevertheless, we were able to estimate, by the viscous parameters of the medium and the maximum speed with which the trapped cell could be moved, that the trapping force imposed on the cell was about 10 pN.

Of course, in this context the method is primarily just a tool. For which scientific problems could it be used? There are many possibilities, but currently we are most interested in measuring the spectra of trapped bioobjects, i.e. combining trapping with spectroscopy. When using neutral trapping wavelengths (i.e. those that are not absorbed by the sample), we could fix the sample in space with minimal influence of surroundings, compared to other fixing methods. It would be most interesting if one could trap single molecules this way, and we believe that some large biomolecules should actually enable it.

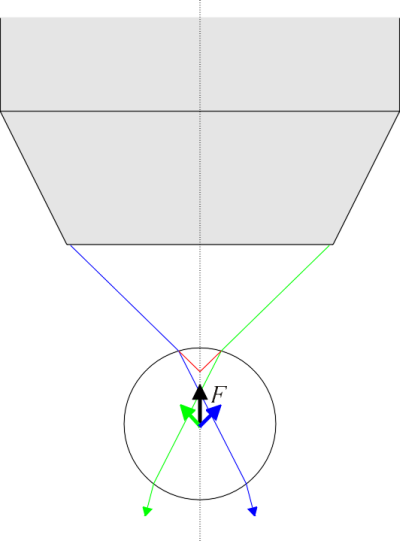
The passage of two rays, belonging to edges of the light cone coming out of the microscope objective, through a sphere with a higher refractive index compared to the surrounding environment. The center of the sphere is currently below the objective focus. Red and green arrows indicate the direction towards which the sphere is pushed by the momentum change of the photons in the ray marked with corresponding color. Black arrow indicates the direction of total momentum delivered to the sphere by photons.